1.1 什么是向量

向量是一种有大小和方向的数学对象。它可以表示为从一个点到另一个点的有向线段。例如，二维空间中的向量可以表示为 (x,y)，表示从原点 (0,0) 到点 (x,y) 的有向线段。

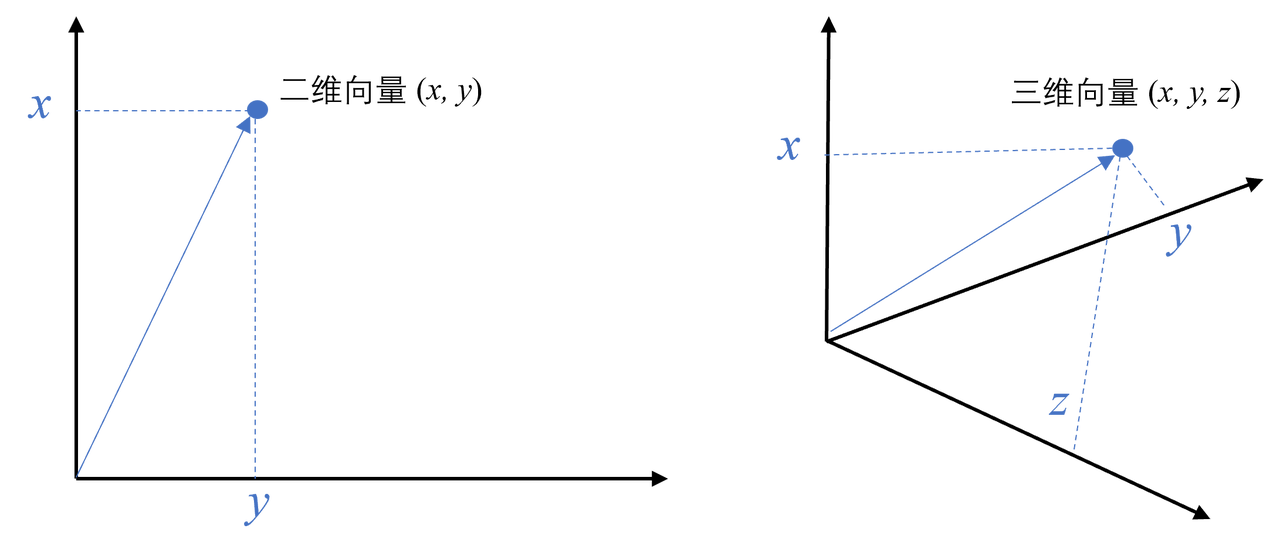
1.2 文本向量

文本向量即将文本数据转换为高维数值向量，将文本转换为向量之后，我们通过两个向量之间的距离来判断两者语义的相似度。

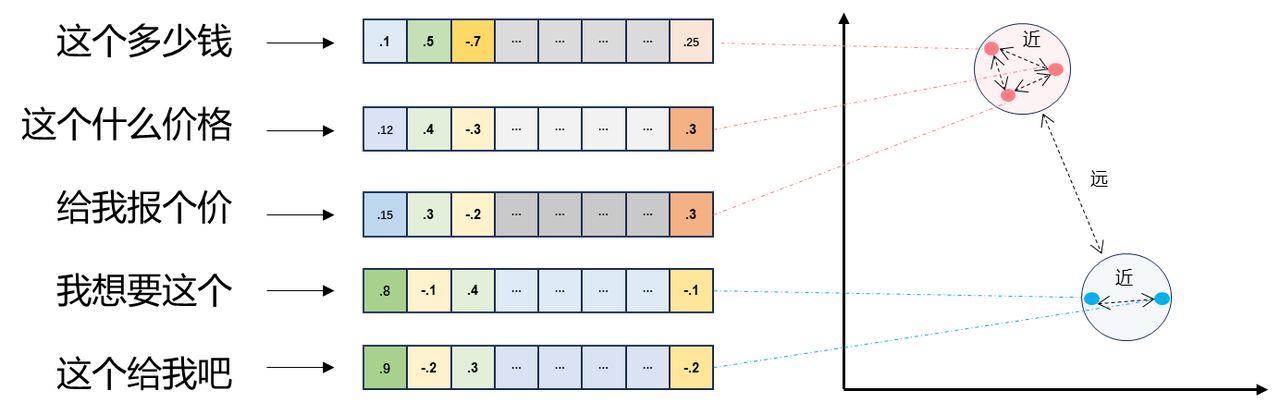
1.3 向量距离与相似度

在嵌入向量空间中，我们通过计算向量之间的距离来衡量语义相似度。

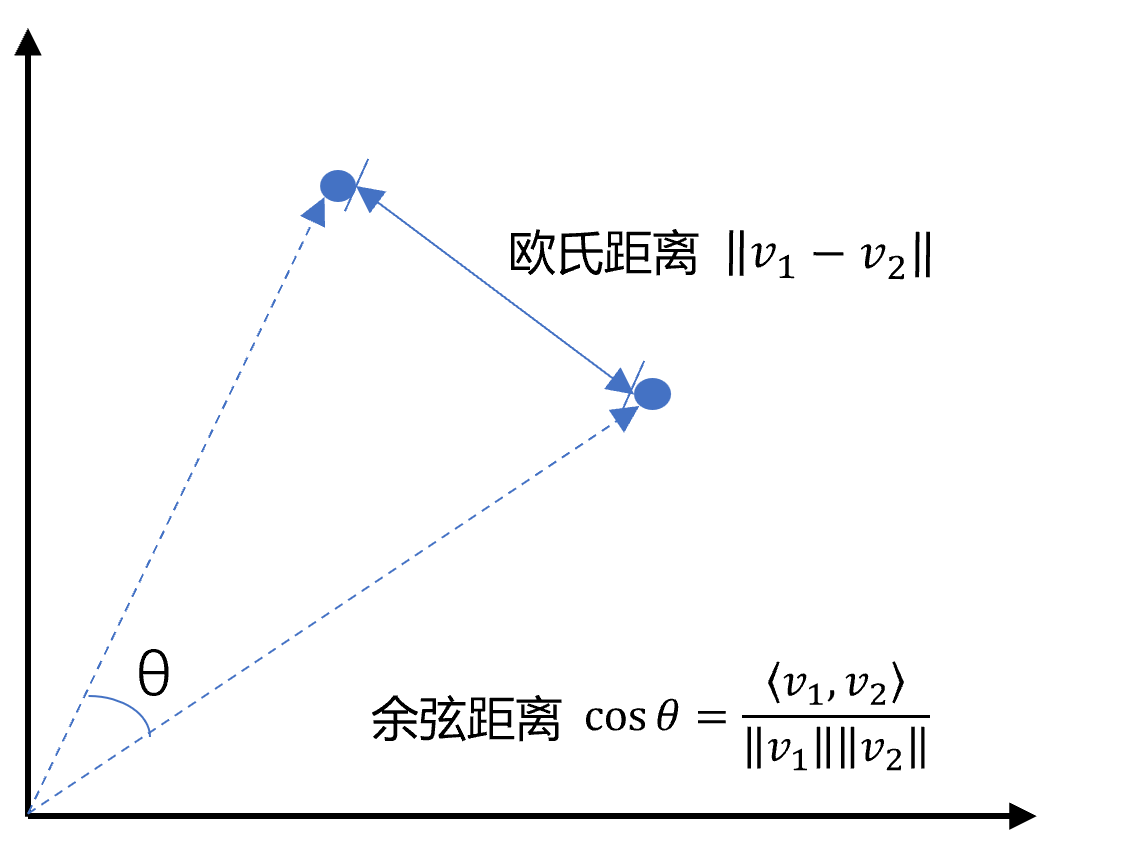
余弦相似度

最常用的相似度计算方法，衡量两个向量之间的夹角余弦：

cos(θ) = (A · B) / (|A| × |B|)

• 取值范围：[-1, 1]
• 1 表示完全相同
• 0 表示正交（不相关）
• -1 表示完全相反

欧氏距离

计算两个向量在空间中的直线距离：

d(A, B) = √(Σ(Aᵢ - Bᵢ)²)

• 距离越小，相似度越高
• 常用于聚类和分类任务

点积（内积）

直接计算两个向量的内积：

A · B = Σ(Aᵢ × Bᵢ)

• 计算简单高效
• 在很多机器学习模型中广泛使用

Python 实现示例

import numpy as np
from numpy import dot
from numpy.linalg import norm

def cos_sim(a, b):
    '''余弦距离 -- 越大越相似'''
    return dot(a, b)/(norm(a)*norm(b))

def l2(a, b):
    '''欧氏距离 -- 越小越相似'''
    x = np.asarray(a)-np.asarray(b)
    return norm(x)

1.4 传统表示方法 vs 嵌入向量

独热编码（One-Hot Encoding）

# 传统方法
"国王"   -> [0, 0, 1, 0, 0, 0, 0, 0]  # 8维稀疏向量
"女王"  -> [0, 0, 0, 1, 0, 0, 0, 0]  # 8维稀疏向量
"男性"    -> [1, 0, 0, 0, 0, 0, 0, 0]  # 8维稀疏向量

# 语义关系无法捕捉
# 国王 - 男性 无法通过向量运算得到 女王

嵌入向量表示

# Embedding 方法
"国王"   -> [0.2, 0.9, -0.1, 0.5]     # 4维稠密向量
"女王"  -> [0.3, 0.8, -0.2, 0.6]    # 4维稠密向量  
"男性"    -> [0.1, 0.8, -0.1, 0.4]    # 4维稠密向量

# 可以捕捉语义关系
# 国王 - 男性 + 女性 ≈ 女王

1.5 简单应用示例

OpenAI Embedding API 调用

def get_embeddings(texts, model="text-embedding-ada-002", dimensions=None):
    '''封装 OpenAI 的 Embedding 模型接口'''
    if model == "text-embedding-ada-002":
        dimensions = None
    if dimensions:
        data = client.embeddings.create(
            input=texts, model=model, dimensions=dimensions).data
    else:
        data = client.embeddings.create(input=texts, model=model).data
    return [x.embedding for x in data]

# 测试向量维度
test_query = ["测试文本"]
vec = get_embeddings(test_query)[0]
print(f"Total dimension: {len(vec)}")
print(f"First 10 elements: {vec[:10]}")

跨语言语义相似度计算

# 支持跨语言语义匹配
query = "global conflicts"

documents = [
    "联合国就苏丹达尔富尔地区大规模暴力事件发出警告",
    "土耳其、芬兰、瑞典与北约代表将继续就瑞典"入约"问题进行谈判",
    "日本岐阜市陆上自卫队射击场内发生枪击事件 3人受伤",
    "国家游泳中心（水立方）：恢复游泳、嬉水乐园等水上项目运营",
    "我国首次在空间站开展舱外辐射生物学暴露实验",
]

query_vec = get_embeddings([query])[0]
doc_vecs = get_embeddings(documents)

print("Query与自己的余弦距离: {:.2f}".format(cos_sim(query_vec, query_vec)))
print("Query与Documents的余弦距离:")
for vec in doc_vecs:
    print(cos_sim(query_vec, vec))

print()

print("Query与自己的欧氏距离: {:.2f}".format(l2(query_vec, query_vec)))
print("Query与Documents的欧氏距离:")
for vec in doc_vecs:
    print(l2(query_vec, vec))