3.1 位置编码的意义

在传统的递归神经网络（RNN）或 LSTM 中，网络通过递归结构自然地处理了输入序列中的顺序信息。每当新的词元进入模型时，它依赖于前一个词元的状态，从而隐式地捕获了输入数据的顺序信息。

但 Transformer 不同，它没有递归结构，而是完全依赖于自注意力机制（Self-Attention）——每个词元可以与序列中任何其他词元直接交互。这种并行处理方式使得 Transformer 无法感知输入的顺序信息。

例如，对于句子"我爱你"和"你爱我"，如果没有位置信息，Transformer 会认为它们是相同的输入。

3.2 位置编码的原理

为解决这个问题，Transformer 引入了位置嵌入：将每个词元的位置信息编码成一个向量，并与词元的词向量相加，使每个输入同时包含语义信息和位置信息。

I    → [0.2, 0.7, ..., 0.1] + PosEnc(0) 
love → [0.5, 0.1, ..., 0.9] + PosEnc(1) 
NLP  → [0.8, 0.3, ..., 0.6] + PosEnc(2)

• 词向量（如 [0.2, 0.7, ..., 0.1]）：表示词元的语义信息
• 位置编码 PosEnc(n)：提供该词元在序列中的位置信息
• 两者相加：输入到 Transformer，使其能够学习到 语义 + 顺序 的联合表示

3.3 位置编码的计算方式

3.3.1 可学习的位置编码（Learnable PE）

让每个位置的编码 PE(pos) 作为可训练参数，通过训练学习最优位置表示。

位置编码矩阵：max_len × d_model
每个位置对应一行可学习的向量

优点：灵活，能适应特定任务

缺点：不具备泛化能力，只能处理训练时见过的序列长度

使用模型：BERT、GPT 系列

3.3.2 固定的位置编码（Sinusoidal PE）

Transformer 原论文使用的方法，通过正弦（sin）和余弦（cos）函数计算：

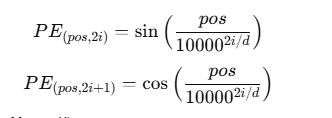
其中：

• pos：词元在序列中的位置（0, 1, 2, ...）
• i：向量的维度索引
• d：嵌入向量的维度（即 d_model）

优点：

• 具有周期性，能推广到任意长度的序列
• 无需训练，计算简单
• 相对位置信息可通过线性变换获得

缺点：表达能力不如可学习的位置编码灵活

3.3.3 两种方式的对比

特性	可学习位置编码	正弦位置编码
参数量	需要额外参数	无需参数
序列长度泛化	受限于训练长度	可推广到任意长度
表达能力	更灵活	固定模式
典型应用	BERT、GPT	Transformer 原论文

3.4 位置嵌入的融合方式

位置编码与词嵌入的结合通常采用相加的方式：

最终输入 = 词嵌入(token) + 位置编码(position)

为什么是相加而不是拼接？

• 维度一致：相加不增加向量维度，保持计算效率
• 信息融合：让语义和位置信息在同一向量空间中交互
• 实验效果：原论文实验表明相加效果与拼接相当，但计算更高效